Skip to contents

Evaluation of forecasts using score decompositions

Source: R/triptych_mcbdsc.R
mcbdsc.Rd

A score decomposition splits the mean score into the three components of miscalibration (MCB), discrimination (DSC), and uncertainty (UNC). Plotting the DSC component against the MCB component allows for a quick visual inspection of predictive performance for many forecasting methods.

Usage

mcbdsc(x, y_var = "y", ..., y = NULL, score = "Brier_score")

as_mcbdsc(x, r)

Arguments

x

A data frame, list, matrix, or other object that can be coerced to a tibble. Contains numeric forecasts, and observations (optional).

y_var

A variable in x that contains observations. Specified as the argument varin dplyr::pull().

...

Unused.

y

A numeric vector of observations. If supplied, overrides y_var. Otherwise, defaults to dplyr::pull(x, y_var).

score

A string specifying the score function. One of: "Brier_score" (default), "log_score", "MR_score".

r

A reference triptych_mcbdsc object whose attributes are used for casting.

Value

A triptych_mcbdsc object, that is a vctrs_vctr subclass, and has a length equal to number of forecasting methods supplied in x. Each entry is named according to the corresponding forecasting method, and contains a list of named objects:

  • estimate: A data frame of the score decomposition.

  • region: An empty list. Adding confidence regions is not yet supported.

  • x: The numeric vector of original forecasts.

Access is most convenient through estimates(), regions(), and forecasts().

See also

Accessors: estimates(), regions(), forecasts(), observations()

Visualization: plot.triptych_mcbdsc(), autoplot.triptych_mcbdsc()

Examples

data(ex_binary, package = "triptych")

md <- mcbdsc(ex_binary)
md
#> <triptych_mcbdsc[10]>
#>             X01             X02             X03             X04             X05 
#> <named list[3]> <named list[3]> <named list[3]> <named list[3]> <named list[3]> 
#>             X06             X07             X08             X09             X10 
#> <named list[3]> <named list[3]> <named list[3]> <named list[3]> <named list[3]> 

autoplot(md)

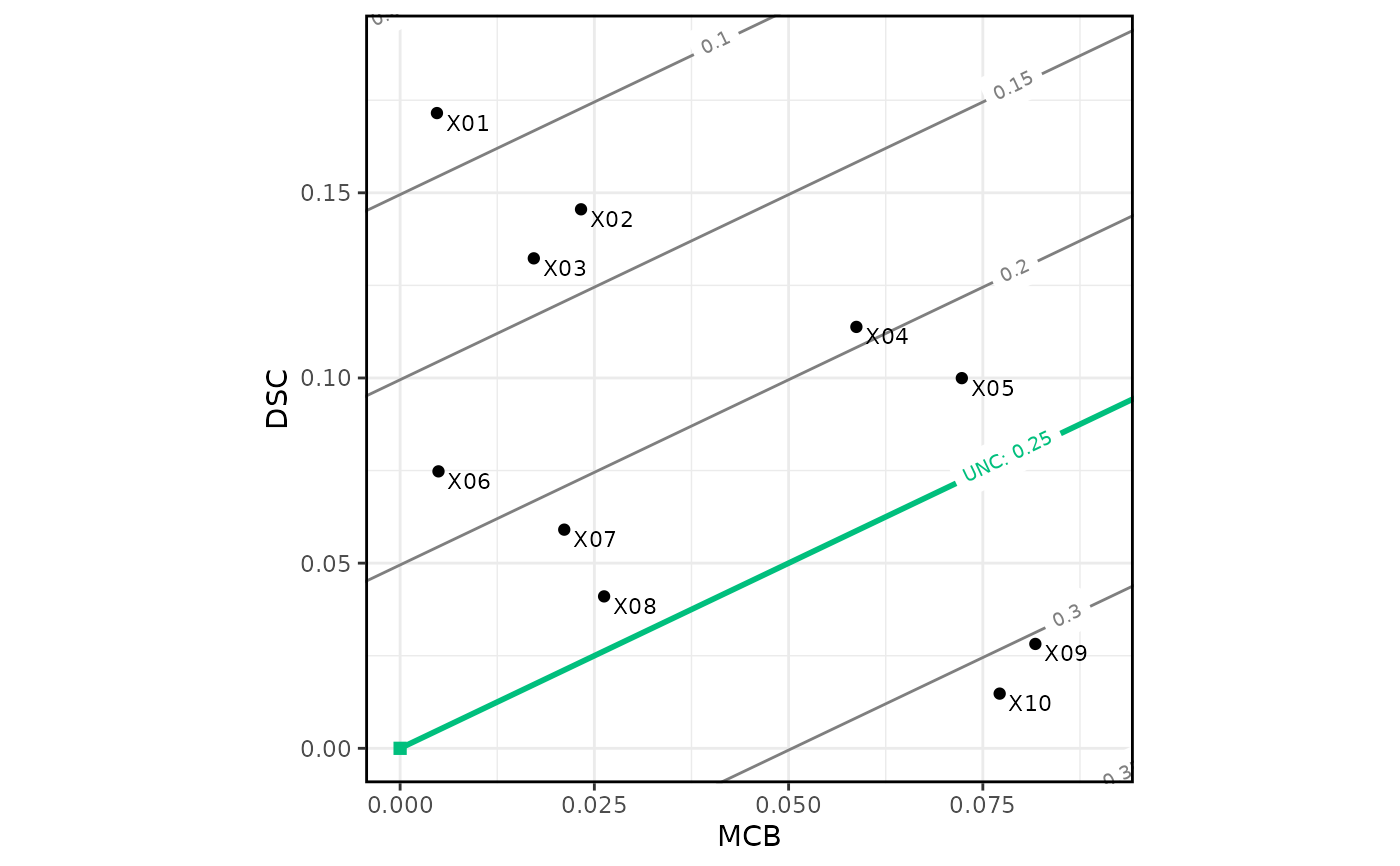estimates(md)
#> # A tibble: 10 × 5
#>    forecast mean_score     MCB    DSC   UNC
#>    <chr>         <dbl>   <dbl>  <dbl> <dbl>
#>  1 X01          0.0827 0.00474 0.172  0.250
#>  2 X02          0.127  0.0233  0.146  0.250
#>  3 X03          0.134  0.0172  0.132  0.250
#>  4 X04          0.194  0.0587  0.114  0.250
#>  5 X05          0.222  0.0723  0.100  0.250
#>  6 X06          0.180  0.00494 0.0748 0.250
#>  7 X07          0.212  0.0211  0.0590 0.250
#>  8 X08          0.235  0.0263  0.0410 0.250
#>  9 X09          0.303  0.0818  0.0282 0.250
#> 10 X10          0.312  0.0772  0.0148 0.250